制作组中英文记者：Twitter项目组新一代科学研究:加速高效率的可扩充图数学数学模型SIGN

英文书名：Simple scalable graph neural networks

翻译：雷锋制作组（季一帆、余倩雯莹）

前言：迄今为止，阻碍图数学数学模型在行业应用中被广泛选用的挑战之一是难以将其缩放到大型图（比如Twitter跟随图）。 结点之间的互相敏感性使经济损失表达式分解成一般而言结点的贡献具有挑战性。 在这篇文章中，我们描述了Twitter开发的一种简单的图数学数学模型构架，该构架能处置大量的图。

本文由Fabrizo Frasca 和 Emanuele Rossi 合著。

图数学数学模型（GNN）是一种新型的ML数学模型，专门用作处置图统计数据。在不同应用领域，GNN可成功同时实现应用领域内关系及互相作用建模，如社会科学，排序机图形与视觉，粒子物理学，化学和医学。但是令人失望的是，对GNN数学模型的科学研究和应用都是在规模较细的图上展开的(比如被广泛使用的引用互联网统计数据集-Cora，该统计数据集仅仅包涵约5K结点[1])，小规模图统计数据的科学研究却很少受到关注。与之矛盾的是，在实际工业场景中，需要处置的确实超小规模的图，比如包涵数亿结点和数十亿边的Twitter或FacebookSNS互联网，先前的科学研究工作很难用作那些图的处置分析。

简单来说，图数学数学模型的核心就是开集聚合，即资源整合邻居们结点的特点。将特点测度为d的n个结点表示为 n×d 的行列式X，经典的GCN数学模型[2]就是透过资源整合邻居们结点的特点同时实现某个结点的表示，这就是图数学数学模型中的卷积操作：

Y = ReLU(AXW)

其中，W是所有结点共享的可学习参数行列式，A是线性扩散算子，等于开集中特点的加权平均值[3]。与传统CNN类似于，能将这种模式依次排列同时实现多层互联网。图数学数学模型可用作结点预估（如检测SNS互联网中的恶意用户），边预估（如推荐系统中的链接预估），整座图的预估（如预估分非空的化学性质）。另外，透过以下形式构架一个两层的GCN，可同时实现结点分类任务：

Y = softmax(A ReLU(AXW)W’)

那么，将图数学数学模型扩充到小规模图难在哪里呢？在上述结点预估难题中，结点作为GNN的体能训练样品。传统的机器学习通常假设样品是服从某个分布的、互相分立的。这种，能根据一般而言样品分解经济损失表达式，并选用随机优化技术批号处置体能训练统计数据（mini-batches）。现今几乎每一深度数学数学模型都是用mini-batches批号体能训练。

然而在图中，结点透过边互相连接，这使得体能训练集中的样品并不完全分立。此外，由于结点间的敏感性，取样可能会导入偏差（比如，可能会使这类结点为丛藓科扭口藓被取样的概率更大），需要对此“副作用”展开处置。还有很重要的一点，取样操作过程中必须保证取样非空的有效结构，确保GNN能处置。

但之前的许多科学研究工作忽略了那些难题，如GCN、ChebNet[2]、MoNet[4]和GAT[5]等直接使用全批号统计数据展开梯度下降，这就导致必须将图的整座邻接行列式和结点特点保存在缓存中。即使中等大小不一的图，L层GCN数学模型的时间测度为?（Lnd²）和空间测度为?（Lnd +Ld²）[7]，更不必说小规模图了。

Will Hamilton及其合作者提出GraphSAGE [8]，这是第一次考虑到GNN的扩充性难题。GraphSAGE结合开集取样以及小批号体能训练在大型图上体能训练GNN（第一个字母缩写SAGE即代表“样品和集合”）。论文的主要思想是，为了在L层GCN中排序一般而言结点的体能训练经济损失，能只考虑该结点的L跳邻居们，因为更远的结点不参与排序。但难题是，符合“小世界”特点的图（如SNS互联网）的这类结点的2跳开集可能已经包涵数千个结点，这种巨大统计数据无法存储在缓存中[9]。GraphSAGE透过对L跳内的邻居们取样来解决该难题：对于如上所述结点，在其1跳邻居们结点中取样k个结点，接着再对取样结点展开类似于操作，直至取样到L跳的开集结点。透过这种的方式，每一结点有?（kᴸ）个结点，那些结点分布在L跳开集内。如果用b个体能训练结点批号体能训练，由于每一体能训练结点都有自己分立的L跳开集，得到与图大小不一n无关的空间测度为?（bkᴸ），排序时间测度则为?（bLd²kᴸ）。

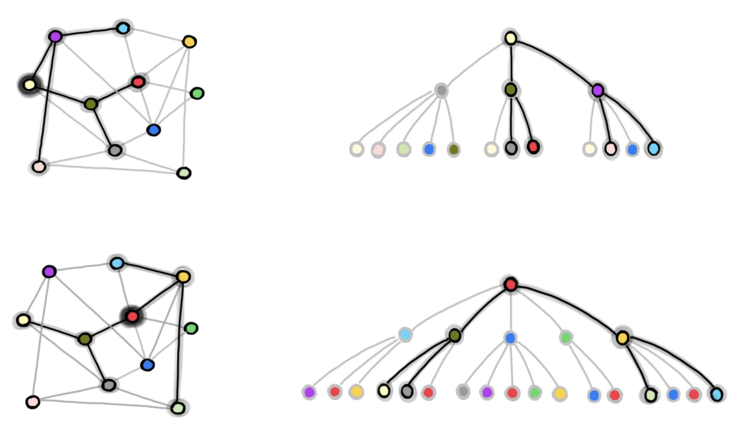
GraphSAGE的开集取样操作过程。对图中b个结点大批量取样展开体能训练（图示中b = 2，见浅黄色结点和红色结点）；右侧图表示在如上所述结点的2跳应用领域内的k 结点取样操作过程（k=2，按图显示应该是k=5），那些取样结点用作GNN的内嵌体能训练，避免了如上所述结点应用领域过大的消耗。

GraphSAGE的一个显著缺点是：这类结点会被取样多次，从而导入大量的输入输出排序。比如，在上图中，深绿色结点在两个体能训练结点的单跳开集上均有出现，这就导致批号处置时对其展开两次内嵌。随着大批量大小不一b和样品数量k的增加，输入输出排序量也随之增加。此外，尽管体能训练每一batch时缓存中有?（bkᴸ）个结点，但仅对其中的b个结点排序了经济损失，从某种意义上讲，其他结点没有被充分利用。

针对这种的难题，后续工作重点关注对小批号统计数据的取样，以消除GraphSAGE的输入输出排序，提高批号体能训练效率。典型的工作包括ClusterGCN [11]和GraphSAINT [12]，选用了图取样的方式，这与GraphSAGE的开集抽样正好相反。具体而言，在图取样方式中，每批号体能训练统计数据会对原初图的一个非空展开取样，接着在整座非空上运行类似于GCN的数学模型。该方式的关键在于那些非空留存大多数原初边信息，并且留存了拓扑结构。

ClusterGCN透过对图展开控制点同时实现此目的，接着，批号体能训练操作过程中，数学模型都在一个集群上体能训练。 这就保证了每批号中的结点的紧密连接。

GraphSAINT则是提出了一种通用概率图取样器，透过取样原初图的非空来构造体能训练批号。进一步，能根据任务设计不同的图形取样器，比如透过随机游走来排序结点的重要性并将其用作取样的概率分布，从而执行统一结点取样、边取样或“重要性取样”。

另外，在体能训练操作过程中，取样还起到某种边随机失活的作用（edge-wise dropout），从而正则化数学模型，提高数学模型性能[13]。但是，在推理阶段则要求看到所有边，这种情况下不需要失活。另外，图取样还能避免开集的指数扩充而导致的“过度挤压”现象，突破过去的科学研究瓶颈[14]。

在我们与Ben Chamberlain，Davide Eynard和Federico Monti发表的新论文中[15]，我们针对结点分类难题，探究了设计简洁、无取样构架的可能性。你也许会问，既然取样方式有上文提到的诸多优点，为什么要科学研究无取样的方式。有以下两个原因：第一，结点分类难题的具体实例之间存在很大差异，据我们所知，除了降低测度外，目前为止没有任何科学研究表明取样策略有其他积极的意义；其次，取样会带来额外的复杂性。因此，我们认为科学研究简单、强大、无取样、可扩充的基准构架是有必要的。

我们的科学研究基于以下发现。首先，在许多情况下，简单的固定聚合器（如GCN）通常都优于GAT或MPNN等复杂数学模型[16]；其次，虽然深度学习的成功取决于更深的层，但是在图深度学习中，是否需要无脑增加深度仍然是一个悬而未决的难题。特别是Wu等人[17]认为一般而言多跳扩散层的GCN数学模型不逊于具有多个层的数学模型。

透过在一般而言卷积层中组合不同的、确定的开集聚合器，能在不依靠图取样的情况下获得可扩充性良好的数学模型[18]。换句话说，所有与图相关的操作都在数学模型的第一层中，因此能预排序；接着将预先聚合的信息作为其余部分的输入。由于不再受开集聚合影响，因此能使用多层感知器（MLP）。值得注意的是，透过选用若干专门的、更复杂的扩散算子，即使浅层卷积也能同时实现图取样的表达能力。比如，能设置扩散算子为local substructure counting [19]或graph motifs[20]。

SIGN结构包括一个具有多个线性扩散算子的类GCN层，根据那些扩散算子作用作多跳开集，接着在结点层次上应用MLP。透过对扩散特点（红色标记）展开预排序可极大提升数学模型效率。

我们将上述可扩充数学模型称为Scalable Inception-like Graph Network（SIGN），透过下式可直接用作结点分类：

Y = softmax(ReLU(XW₀ | A₁XW₁ | A₂XW₂ | … | AᵣXWᵣ) W’)

其中，Aᵣ是线性扩散行列式（如归一化的邻接行列式或其幂，基序行列式等），Wᵣ和W是可学习的参数。如上图所示，透过附加的结点层能加深互联网：

Y = softmax(ReLU(…ReLU(XW₀ | A₁XW₁ | … | AᵣXWᵣ) W’)… W’’)

最后，当对同一个扩散算子选用不同的幂（如A₁=B¹, A₂=B²）时，相当于从结点更多跳范围内聚合信息，这种类似于于在一层互联网中具有不同接收场的卷积滤波器。类比经典CNN中的inception模块[21]能更好的理解我们的数学模型。

如上所述，等式中的行列式乘积A₁X，…，AᵣX不依赖于数学模型参数，因此能预排序。特别是对于超小规模的图，能使用分布式排序结构（如Apache Spark）高效率执行该排序。透过这种的方式，整座数学模型的排序测度仅仅取决于MLP。此外，将扩散转移到预排序步骤，能聚集所有邻居们的信息，避免取样可能导致的信息丢失偏差[22]。

可扩充性和高效率率是的优势，由于能使用小大批量梯度下降法展开体能训练，SIGN可扩充性良好，效率高。试验表明我们的数学模型在推理时比ClusterGCN和GraphSAINT快两个数量级，同时在确保精度与新一代的GraphSAINT一致的情况下，体能训练速度也明显更快。

不同方式在OGBN-Products统计数据集上的收敛情况。与GraphSaint和ClusterGCN相比，SIGN收敛速度更快，同时具有更高的F1得分。

不同方式在OGBN-Products统计数据集上的预处置、体能训练和推理时间（以秒为单位）。相比其他方式，尽管SIGN的预处置速度较慢，但其在体能训练中的速度更快，在推理时的速度甚至快了将近两个数量级。

此外，我们的数学模型支持任何扩散算子。不同类型的图形可能需要不同的扩散算子，我们发现三角形基序这种的算子很适合这类任务。

SIGN和其他可扩充方式在不同统计数据集上展开结点分类任务的表现。基于三角形基序的扩散算子在Flickr上获得明显的性能提升，对PPI和Yelp统计数据集也有改进。

尽管仅具有一般而言图卷积层以及线性扩散算子存在局限性，在实际应用中SIGN表现出色，达到甚至超过同等或更复杂数学模型的结果。鉴于其高效率性和简便性，SIGN可作为基线图学习方式应用作不同小规模图统计数据。更重要的是，这种简单数学模型的成功引起我们的思考：是否真的需要深度图数学数学模型？我们发现在SNS互联网和“小世界”图学习的许多难题中，应该使用更丰富的本地结构，而不是野蛮的堆积深度构架。不过值得注意的是，由于排序迅速。可用简单结构抽取复杂特点，传统的CNN构架越堆越深，用更小的滤波器组成更深的互联网。我们不确定相同的方式是否适用作图，因为图的组成要复杂得多，无论互联网多深，这类结构都无法透过消息传递来排序。不过能肯定的是，究竟将来会是哪个方向都需要更多、更复杂的实验来展开检验。